Sparse Matrix Imputation Using Multi-Objective Loss Function Balancing
Project Overview
Current sparse matrix modeling techniques, like Principal Component Analysis (PCA), often use low-rank approximations to convert sparse matrices into denser, lower-dimensional forms for deep learning models. While these methods enhance computational efficiency, they struggle to preserve the nuanced relationships in the original data, which is crucial for tasks requiring structural or contextual information, such as temporal analysis, sensor networks, and various scientific fields involving high-dimensional or structured data.
We propose a model that processes sparse matrices directly, learning intrinsic patterns and relationships without relying on low-rank approximations. Our hypothesis is that inputting sparse matrices into autoencoders (AEs) often biases the model toward zero-value areas, neglecting patterns in data-dense regions, thus compromising the reconstruction of significant information. To address this, we propose a multi-objective loss function that balances learning from both data-dense and sparse regions, dynamically adjusting the loss functions to capture meaningful patterns within sparse matrices effectively.
Background and Motivation
Sparse matrix imputation is a critical task in modern data science, particularly for applications involving spatio-temporal data, such as traffic modeling, environmental monitoring, and sensor networks. Traditional methods like PCA and low-rank approximations improve computational efficiency but often fail to preserve the nuanced relationships in high-dimensional structured data.
The advent of deep learning, specifically autoencoders (AEs), has provided new opportunities to directly process sparse matrices. However, existing approaches often suffer from overfitting to zero-value areas, neglecting meaningful patterns in data-dense regions due to their relative scarcity. This imbalance limits their ability to generalize across diverse datasets and spatio-temporal scenarios.
Our motivation is to address these gaps by introducing a dynamic, multi-objective loss function to enable balanced learning from both sparse and dense regions. This approach ensures robust imputation, preserves intrinsic data structures, and improves generalization across tasks.
Approach and Methods
Vision Transformer Architecture
Our solution utilizes a Vision Transformer (ViT) architecture combined with learnable positional and time embeddings to effectively model both spatial and temporal dependencies in sparse matrices. The ViT model divides the input matrix into smaller patches and processes them as tokens, leveraging the self-attention mechanism to capture global dependencies. This approach is particularly suited for sparse matrices as it:
- Preserves the structure of the matrix while modeling long-range dependencies
- Adapts seamlessly to matrices with varying sparsity levels
Multi-Objective Loss Function with GradNorm
The key innovation is integrating GradNorm to dynamically balance the contributions of nonzero and zero-area losses during training. To address the imbalance observed with traditional models like UNet, we incorporate GradNorm, a dynamic loss-balancing method that scales loss terms based on their gradient magnitudes.
We partition the loss function into two components:
- Loss for nonzero regions: Focuses on minimizing the reconstruction error in data-dense areas
- Loss for zero regions: Focuses on accurately reconstructing sparse (zero) areas
The total loss is given by: \(L = w_{nz} \cdot L_{nz} + w_z \cdot L_z\)
By dynamically scaling $w_{nz}$ and $w_z$, GradNorm ensures that both nonzero and zero regions are learned effectively. If one loss dominates (e.g., large gradients for $L_{nz}$), GradNorm reduces its weight while increasing the weight of $L_z$, encouraging balanced learning.
Experiments & Dataset
The dataset spans a 3-month period from April to June 2024, consisting of traffic flow data across various intersections and roads within Taipei City. Each data point includes traffic flow count, geographical coordinates, and precise timestamps.
To simulate realistic sparsity conditions, we randomly masked 80% of the non-zero entries, reflecting scenarios where sensor failures or missing records are commonplace. The dataset was split into training (70%), validation (15%), and testing (15%) sets, respecting temporal order to prevent leakage of future information.
Data Processing with H3 Geo-partitioning
We employed the H3 geo-partitioning method, a hexagonal hierarchical spatial indexing system developed by Uber. H3 partitions the geographical space into uniform hexagonal cells, ensuring consistent spatial distribution and preserving geographical proximity.
The traffic flow data was vectorized by mapping each measurement to its corresponding H3 cell based on geographical coordinates, converting the spatial-temporal data into a series of matrices where each matrix represents a snapshot of traffic flow across Taipei at a specific time.
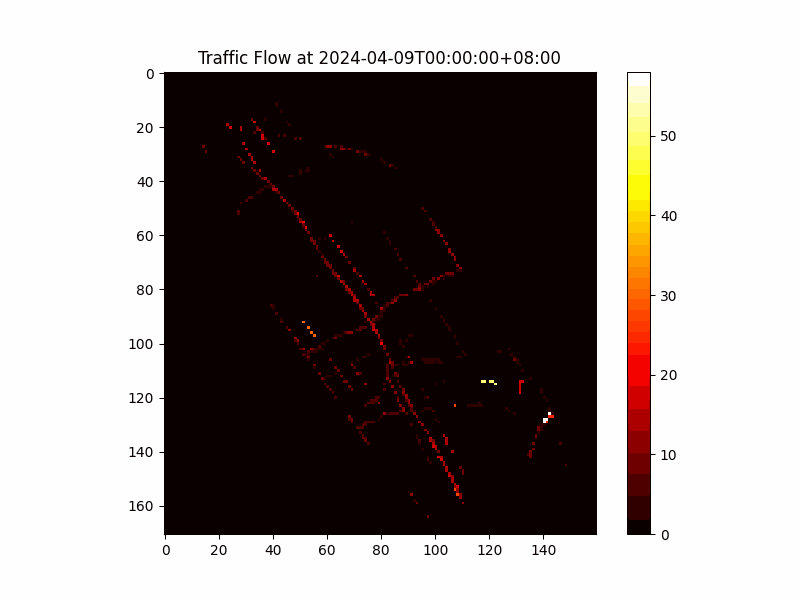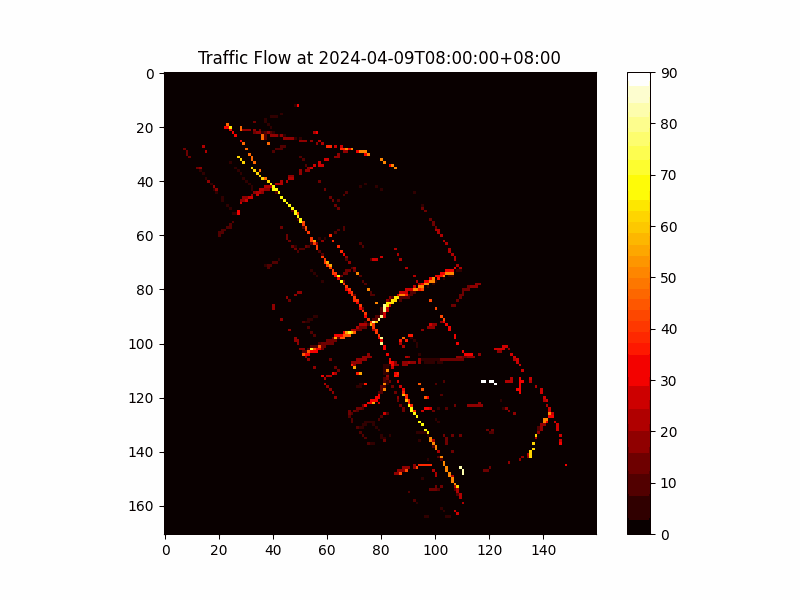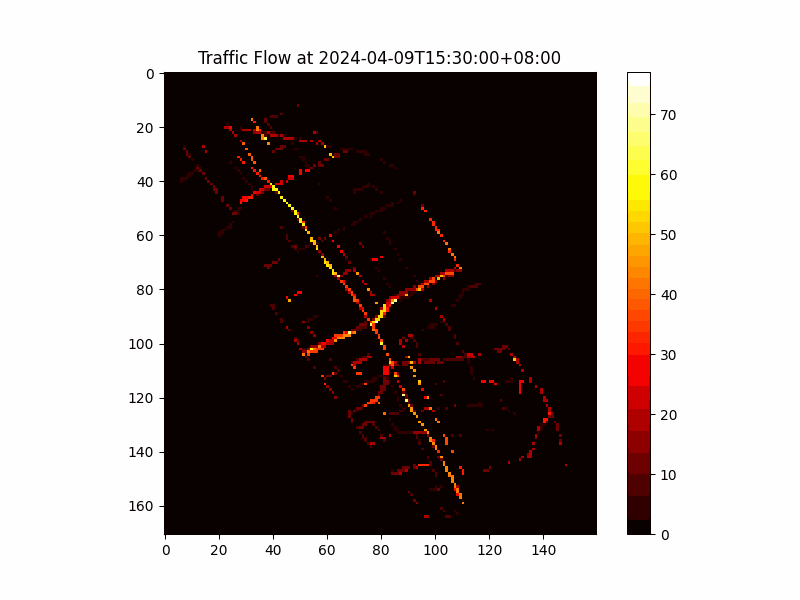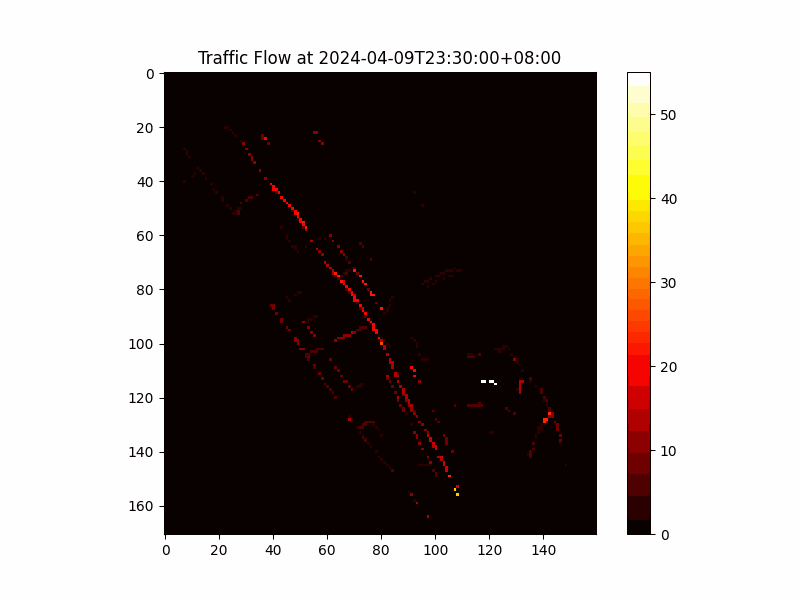
Figure 1: Vectorized Traffic Flow Data in H3 Cells
Experimental Design
We conducted experiments with three different approaches:
- Baseline: Neighbor-Averaging Mask Reconstruction
- Random masking of 80% of non-zero values
- Prediction by averaging values of valid neighboring cells
- Results showed severe limitations in capturing meaningful spatial relationships

Figure 2: Neighbor-Averaging Mask Reconstruction Results
- UNet with a Single Loss Function
- Encoder-decoder architecture with skip connections
- Mean Squared Error (MSE) between reconstructed and original matrices
- Results showed overfitting to zero areas, failing to capture detail in high-traffic zones
- Transformer with GradNorm (Our Proposed Solution)
- ViT architecture with learnable positional and time embeddings
- Dynamic loss balancing using GradNorm
- Results demonstrated balanced learning across both sparse and data-dense regions

Figure 3: Imputation Example from our Transformer with GradNorm approach
Results and Analysis
Balanced Learning
GradNorm allowed the model to prioritize learning from the nonzero areas during the early stages of training. Over time, it dynamically balanced the focus between nonzero and zero-area imputations, enabling the model to learn both effectively. This approach not only ensured comprehensive training but also enhanced the accuracy of nonzero-area imputations.
Generalizability
Our model was trained with matrices where 80% of the non-zero entries were masked. Despite this highly sparse training scenario, the model demonstrated strong generalization capabilities when applied to input matrices with lower masking ratios. When tested on inputs with reduced levels of missing data (e.g., 50% or 60% masked), it not only maintained its performance but actually improved upon it.
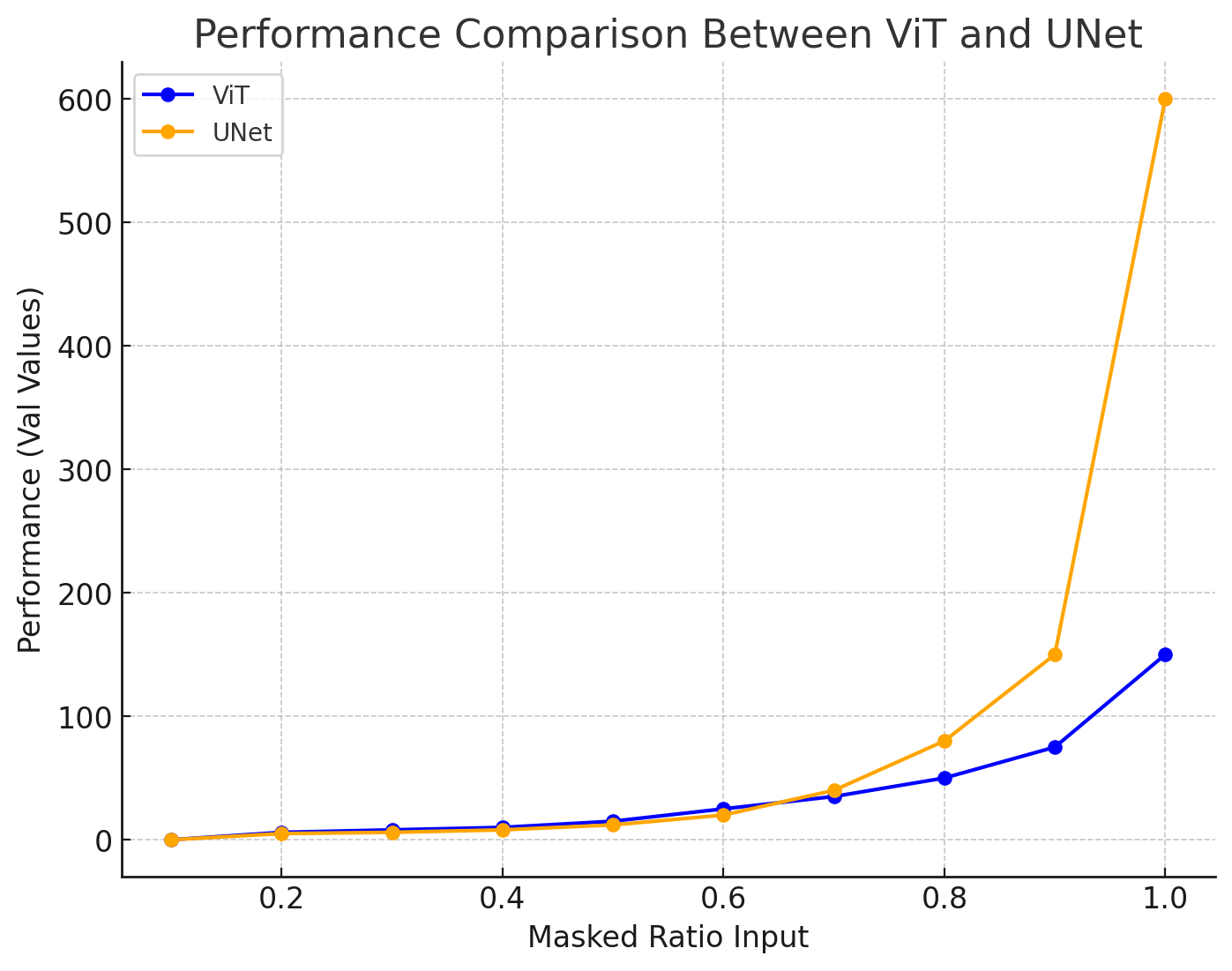
Figure 4: Performance Comparison between UNet and ViT Models at Different Masking Ratios
Strategic Sampling
During the experiment, we observed that certain traffic flow data in the city contained more critical information for accurate imputation. We applied a greedy approach and a Genetic algorithm to identify which elements inside the matrix are critical for improving accuracy. With a masked ratio above 90%, our method achieved an MSE error of 31.82, a twofold improvement compared to random sampling.
This finding suggests that the model relies more heavily on certain “key” nodes in the transportation network. These insights could inform sensor placement strategies or highlight particularly influential regions of a city’s traffic flow, aiding urban planners and transportation engineers.
Geospatial Imputation Demonstration
The model’s ability to use sparse yet informative data points—coupled with its learned understanding of the city’s road network—allows for accurate geospatial imputations. By observing only a small fraction of the matrix, the model infers missing values across large, masked-out areas, effectively reconstructing complex spatial structures.
Figure 5: Geospatial Imputation Demonstration Over Time and Space
Applications & Future Work
Key Contributions
- Direct Sparse Matrix Processing: Moving beyond traditional low-rank approximations by directly modeling sparse matrices without compressing them
- Dynamic Loss Balancing with GradNorm: Introducing a multi-objective loss function that dynamically adjusts its focus between zero and non-zero regions
- Integration of Transformer Architectures and Time Embeddings: Demonstrating that global attention mechanisms can effectively handle complex spatial-temporal dependencies in highly sparse traffic data
- Empirical Validation and Insights for Urban Analysis: Providing insights for urban planners and engineers on sensor placement and network design
Applications
This research has applications in:
- Urban traffic flow prediction and analysis
- Sensor network optimization and placement strategies
- Environmental monitoring with incomplete data
- Any domain involving sparse spatio-temporal data
Limitations
- Computational Overhead: The Transformer-based model, while providing improved accuracy, introduced higher computational and memory requirements
- Limited External Factors: Our current experiments did not integrate external variables such as weather conditions, events, or public holidays
- Fixed Geographic Partitioning: The H3 partitioning scheme may not adapt seamlessly to heterogeneous urban topologies
Future Work
- Efficiency and Scalability Improvements: Developing more efficient attention mechanisms or model architectures
- Incorporation of External Contextual Factors: Integrating complementary data sources to enrich the model’s representation of urban dynamics
- Adaptive Spatial Partitioning and Sensor Placement: Investigating adaptive or learned partitioning schemes
- Transferability and Domain Adaptation: Extending the model to other cities or domains to test its adaptability and robustness